Linear Model Cheating Sheet

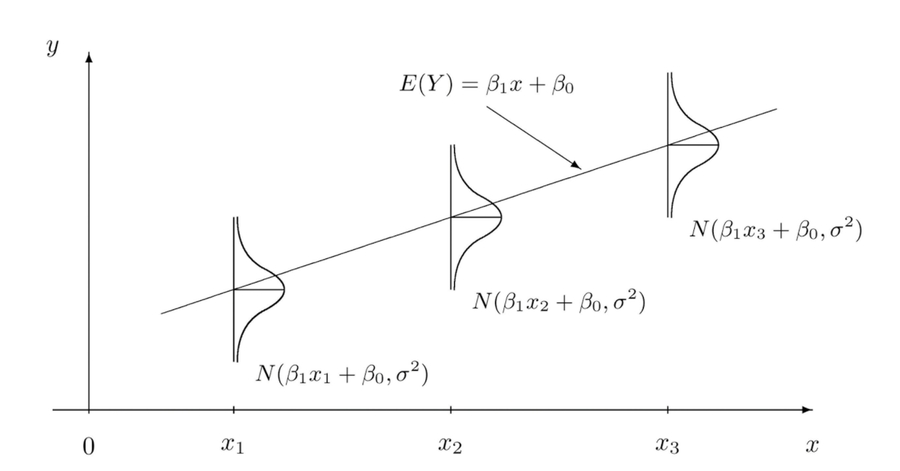
Linear Regression

Definition

• Linear regression is a linear model, which a linear relationship between the input and output . More technical, we can consider $y$​ can be a linear combination of $X$​

Representation

• $Y= \beta_0+\beta_1X+\epsilon$

How to determine this model?loss function？

• 最小二乘法least square推导loss function

  • $Loss =\min_{\beta_0,\beta_1} \sum_{i=1}^{n}(y_i-\beta_0+\beta_1X_i)^2$

• 最大似然估计MLE（maximum likelihood estimation）推导loss function

  • what is mle?

    • 用参数估计的方法，在有了一定的观测值之后，来找parameter，让我们可以最有可能看到我们观测值，让我们可以最大程度放大我们的观测值

    • method

    • estimating the parameters

    • statistical model

    • given observation

    • finding the parameter values

    • maximize the likelihood(making the observation given the parameters)

  • 推导过程（Y follws什么distribution？）

    • $p(Y_i\vert X_i)=\frac{1}{\sigma(2\pi)}e^{-\frac{1}{2\sigma^2}(Y_i-\bar{\beta}_0-\bar{\beta}_1X_i)^2}$

    • $L(\bar{\beta}_0,\bar{\beta}_1,\sigma^2)=p(Y_1,\cdots,Y_n\vert X_1,\cdots,X_n)=\frac{1}{\sigma^{n}(2\pi)^{n/2}}e^{-\frac{1}{2\sigma^2}\sum_{i=1}^n(Y_i-\bar{\beta}_0-\bar{\beta}_1X_i)^2}$

  • 

• 两者的关系

  • 当他们在linear regression下的assumption下，这两个方法得到结果是相通的

  • one is from statistics, and the other one is from optimization

• 一些提醒

  • noise是数据造成的，是inherent bias. error是模型造成的，是人为的。是两个不同的概念

How is the performance of this model?

• （这个是来看模型自己的好坏，评价自己的参数）

• 我们只能系统的保证其不会偏差（$E(Y)=\mu$​​​​​​​​）

• null hypothesis : $\beta_1=0$

  • 目的是从统计上来判断这组数据和population相差多少，assessing the accuracy of the coefficient estimation,可以使用 ppp​-value 或者是 confidence interval

  • 选择的统计量$t=\frac{\hat{\beta}_1-0}{SE(\hat{\beta}_1)}$​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​distribution with $n-2$ degrees of freedom assuming $\beta_1=0$​​​​​​

How can we compare this model with others model?

• (这个相当于模型外的判断模型的好坏 i.e. the extent to which the model fits the data)

• assessing the overall accuracy

• $RSE=\sqrt{\frac{1}{n-2}RSS}=\sqrt{\frac{1}{n-2}\sum_i^{n}(y_i-\hat{y}_i)^2}$

• $R^2=\frac{TSS-RRR}{TSS}=1-\frac{RSS}{\sum_i^{n}(y_i-\hat{y}_i)^2}$

  • where TSSTSSTSS​​​ is total sum of squares, RSSRSSRSS​​​ is the residual sum of squares(对误差的多少)

  • 当是simple regression时，他相同于correlation

  • 这里相当于 proportion of variability in that can be explained using ( 的变化中能够被解释的部分的比例 )

Multilinear Regression

Logistic Regression

图形/值域的理解

• 采用这个方法：$x \rightarrow p(x) \rightarrow y$

  • 首先用 $x$​去拟合 概率$p(x)$​​​​

  • 然后用$p$​再去拟合$y$​ （采用threshold）

  • $p(x)=\frac{e^{f(x)}}{1+e^{f(x)}}=\frac{1}{1+e^{-f(x)}}$

• $Y$​是得病不得病，$p$​是相当于肿瘤的指数， $X$​是关于肿瘤的input（size，位置，etc）

  • $p(Y=y_i)=p^{y_i}(1-p)^{1-y_i},\ 0<p<1,\ y_i=0,1$

  • $log\frac{p(X)}{1-p(X)} = \beta_0+\beta_1X$

How to determine this model?loss function？

• Using MLE to get the loss function（面试必考题）

  • Key：Y fellows 什么distribution？

    • $P(Y=y_i\vert X) = p^{y_i}(1-p)^{1-y_i}, \ 0<p<1,\ y_i=0,1$

  • $p=h_{\beta}(x_i)=\frac{1}{1+e^{-\beta_0+\beta_1x}}$​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​

  • $L(\hat\beta_0,\hat \beta_1)=\Pi_{i=1}^{n}P(Y_i \vert X_i)= \Pi_{i=0}^n p^{y_i}(1-p)^{1-y_i}=\Pi_{i=0}^n {h_{\beta}(x_i)}^{y_i}(1-h_{\beta}(x_i))^{1-y_i}$

• 如何调参呢？有没有类似与linear的t distribution之类的？

How is the performance of this model?

• t distribution？something？

How can we compare this model with others model?

• link: Confusion matrix/AUC

Compare with linear regression

• 关于y的assumption

• Step1： ‘Given ，得的distribution’——这是机器学习模型利用数据可以解决的问题

• Step2: ‘根据的distribution，得到的取值’——判断怎么用是你的问题

Multiple Logistic Regression

• $p(x)=h_{\beta}(x_i)=\frac{1}{1+e^{g(x)}}, \ \textit{where }\ g(x)=\beta_0+\beta_{1,1}x_1+\beta_{1,2}x_1^2+\beta_2x_2$

• 你会面对一个（overfit/underfit）的问题：

  • 模型复杂度对分类效果的影响

  • 模型复杂提到，可以更好的对应training data，但是对testing data不一定好

  • 过度拟合就是overfitting，但是过少可能就underfitting

• 很多时候，多分类问题可以比较成为多个两分类问题，两两二分类来做

Regularization——Ridge regression/Lasso regression

SVM

• $E((w^Tx+b,0)_{\max})$

• Maximum margin classifier $\max \frac{1}{\vert \vert w \vert \vert},\qquad s.t. y_i(w^Tx_i+b)\geq 0,\qquad i=1,\cdots$

• $\min \frac{1}{2}\vert\vert w \vert\vert^2,\qquad s.t. y_i(w^Tx_i+b)\geq 1,\qquad i=1,\cdots,n$

  • dual $\mathcal{L}(w,b,a)=\frac{1}{2}\vert \vert w\vert \vert^2-\sum_{i=1}^n \alpha_i(y_i(w^Tx_i+b)-1)$

  • $\mathcal{L}(w,b,a)=\sum_{i=1}^n\alpha_i-\frac{1}{2}\alpha_i\alpha_jy_i y_jx_i^T x_j$ and $w=\sum_{i=1}^n\alpha_iy_ix_i$

• 换成核估计

  • $f(x)=\sum_{i=1}^Nw_i\phi_i(x)+b$ 转换成为 $f(x)=\sum_{i=1}^l\alpha_i y_i \langle \phi(x_i), \phi(x) \rangle+b$

  • $\alpha$​​​​​​可以由dual 来求

    • $\max_{\alpha}\sum_{i=1}^n \alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle \phi(x_i)\phi(x_j)\rangle \qquad s.t. \alpha_i \geq 0,i=1,\cdots, n; \sum_{i=1}^n\alpha_iy_i=0$

    • $\max_{\alpha}\sum_{i=1}^n \alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_ix_j \qquad s.t. \alpha_i \geq 0,i=1,\cdots, n; \sum_{i=1}^n\alpha_iy_i=0$